Basics of Logic: Lesson-02
Cause & Effect Reasoning
Cause & Effect:
Let’s say,
Maria is good in logic, so she is good in reasoning.
Cause = Maria is good in logic
Effect = She is good in reasoning.
Similarly,
If rain fall, then soil wet.
Cause = Rain fall
Effect = Soil wet.
At this stage, you should start thinking critically. The above argument is a MUST be true argument, which says If rain fall, then soil wet. Because rain fall always results soil wet.
Can you think “Some rain fall does not result soil wet?” Well, the answer is no, so this statement is false.
Therefore, All rain fall results to soil wet.
This is a General Believe or a fact, which cannot call into question.
But what can be called into question is the reverse scenario.
Note that soil is wet because of raining. But the reverse case is not MUST be true scenario. i.e,
As the soil wet, therefore, the rain must have fallen.
As discussed earlier, you must believe that ‘rain fall’ is a smaller circle inscribed (i.e completely inside) in larger circle ‘soil wet’. Because rain fall always result soil wet. But if somebody see wet soil, it does not necessarily due to the rain fall. The soil wet may be due to some other reason or reasons.
Remember that the game of cause and effect is very complex. In advance level study plan, we’ll discuss this in such a manner that you’ll feel much confident while solving arguments related to cause & effect. So at this stage, we just need to learn basics. So let’s go ahead.
Valid vs Invalid argument:
Let’s understand valid and invalid argument.
A valid argument has a valid conclusion, while an invalid argument has an invalid conclusion. For instance,
Example 1:
All primates have heart.
All humans are primates
⇒ All humans have heart. (Which is valid and true.)
Similarly,
All breathing things are living organisms
All humans are breathing
⇒ All humans are living organisms. (Which is valid and true.)
Valid: Which can be logically and correctly drawn from the premises (or given information).
True: Which is generally believed as true.
On other hand,
Example 2:
All journalists are eloquent
Some politicians are eloquent
⇒ Some politicians are journalist. (Which is invalid.)
This conclusion is invalid because in order to have a valid conclusion, the statement MUST be true, rather than COULD be true.
All journalists are eloquent ⇒ Circle J is inscribed in circle E
Some politicians are eloquent ⇒ Circle P is either inscribed in or at least overlapped with circle E.
This is because Some = partial or total
Based on this information, think critically whether “Some politicians are journalist” MUST be true?
You’ll be right, if your answer is no. Because it is also possible that Circle P do not overlap Circle J at all, but is inscribed or overlapped with Circle E. Therefore, the conclusion is not valid.
Similarly,
All dogs are mammals
Non of the cats is dog
⇒ Non of the cats is mammals (Which is invalid and false.)
This conclusion is also invalid, because the conclusion is not MUST be true. Therefore, we cannot infer ‘Non of the cats is mammals’ from the given information. The reason is same as discussed above. Circle D is inscribed in Circle M, while Circle C and Circle D are disjoint (i.e not overlap). So it might be possible that Circle C overlap Circle M, despite remain disjoint with circle D as shown below:
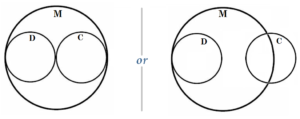
Similarly,
Some leopards have horns.
Some snakes are leopards.
⇒ Some snakes have horns. (Which is invalid and not true.)
General types of Reasoning:
i. Deductive Reasoning
ii. Inductive Reasoning
Deductive reasoning:
Deductive reasoning moves from general to specific (i.e broad to narrow). This is basically deduced from broad to narrow. Furthermore, in deductive reasoning, conclusion is drawn based on premises that are generally accepted as true. For instance,
Honesty is the best policy
Government is adopting honesty
⇒ Government is adopting the best policy
Inductive reasoning:
Inductive reasoning moves from specific to general i.e it induced from narrow and then conclude to broad. Furthermore, in inductive reasoning, conclusion is drawn based on premises that are based on hypothesis and collected from some previous observations. Here the conclusion might be a prediction, a forecast, or some sort of theory in generalized form. For instance,
In last 2 matches, Mr A got injured while playing football.
Mr A will play all the next matches of football
⇒ Mr A will get injured in all the next matches of football.
Remember that,
Positive premise + Positive premise = Positive conclusion
Positive premise + Negative premise = Negative conclusion
Negative premise + Negative premise = Negative conclusion
For instance,
People of Country A are not US citizens
US citizens are not terrorist
⇒ People of Country A are terrorist. (Which is invalid)
Note that this positive conclusion has drawn from two negative premise. Therefore, the conclusion is invalid.





